Vektor

Im allgemeinen Sinn versteht man in der linearen Algebra unter einem Vektor (lateinisch vector „Träger, Fahrer“) ein Element eines Vektorraums.

Dieser Artikel beschäftigt sich überwiegend mit Vektoren im geometrischen Sinn und mit Vektoren als Elementen des „Tupelraums“ $\mathbb {R} ^{n}$.

Im engeren Sinne versteht man in der analytischen Geometrie unter einem Vektor ein mathematisches Objekt, das eine Parallelverschiebung in der Ebene oder im Raum beschreibt. Ein Vektor kann durch einen Pfeil dargestellt werden. Dabei beschreiben Pfeile, die gleich lang, parallel und gleich orientiert sind, denselben Vektor. In kartesischen Koordinaten werden Vektoren durch Zahlenpaare (in der Ebene) bzw. Zahlentripel (im Raum) dargestellt, die oft untereinander (als „Spaltenvektoren“) geschrieben werden. Vektoren können addiert und mit reellen Zahlen (Skalaren) multipliziert werden.

Eng verwandt mit den geometrischen Vektoren sind vektorielle Größen in der Physik. Das sind physikalische Größen, die einen Betrag und eine Richtung besitzen und oftmals durch Pfeile dargestellt werden, deren Länge dem Betrag der Größe entspricht. Beispiele dafür sind Geschwindigkeit, Beschleunigung, Impuls, Kraft, elektrische und magnetische Feldstärke.

Motiviert von der Koordinatendarstellung der geometrischen Vektoren werden oft auch $n$-Tupel reeller Zahlen, also Elemente des $\mathbb {R} ^{n}$, als Vektoren oder auch als Koordinatenvektoren bezeichnet. Dies ist dadurch gerechtfertigt, dass jeder $n$-dimensionale reelle Vektorraum isomorph zum Vektorraum $\mathbb {R} ^{n}$ ist. Beispiele solcher Verwendung des Vektorbegriffs finden sich namentlich in der Wirtschaftsmathematik.

Geschichte

Begründet wurde die Vektorrechnung von Hermann Günter Graßmann, der 1844 seine Lineale Ausdehnungslehre veröffentlichte, ein über 300 Seiten starkes Buch. Als Vorläufer gelten u. a. René Descartes und August Ferdinand Möbius, ein Schüler von Carl Friedrich Gauß. Um 1850 benutzte der irische Mathematiker Matthew O’Brien die Vektorrechnung zur Beschreibung mechanischer Sachverhalte, blieb aber weitgehend ignoriert. Kurz darauf entwickelte William Rowan Hamilton seine ähnliche Theorie der Quaternionen, die er 1853 in dem Buch Lectures on Quaternions und 1866 in dem Werk Elements of Quaternions publizierte, wobei er die bahnbrechenden Leistungen Graßmanns ausdrücklich anerkannte. In Deutschland wurde die Vektorrechnung insbesondere durch Vorlesungen und Bücher von Alfred Bucherer, August Föppl, Carl Runge, Fischer, Wladimir Ignatowski und Richard Gans verbreitet.

Schreibweise

Variablen, die für Vektoren stehen, werden vor allem in der Schulmathematik und in der Physik häufig mit einem Pfeil gekennzeichnet (${\vec {a}},{\vec {v}}$). Vor allem im englischsprachigen Raum werden sie auch fett geschrieben ($\mathbf {v}$, ${\boldsymbol {v}}$ oder v). In Handschriften wird dies häufig durch Unterstreichung (${\underline {v}}$) oder Ähnliches repräsentiert. Früher war teilweise auch die Schreibweise mit kleinen Frakturbuchstaben (${\mathfrak {a}},{\mathfrak {b}},{\mathfrak {v}}$) üblich, handschriftlich durch deutsche Schreibschrift bzw. Sütterlinschrift wiedergegeben. Häufig gewählte Buchstaben sind ${\vec {a}},{\vec {b}},{\vec {c}}$ und ${\vec {u}},{\vec {v}},{\vec {w}}$. Der entsprechende lateinische Buchstabe ohne Vektorkennzeichnung steht meist für die Länge (den Betrag) des Vektors: $v=|{\vec {v}}|$

Geometrie

Definition

Verschiebung des Dreiecks ABC durch Verschiebung der Punkte um ${\vec {v}}$

In der Geometrie versteht man unter einem Vektor ein Objekt, das eine Verschiebung einer Punktmenge in der Ebene oder im Raum beschreibt. Eine Verschiebung kann durch einen Pfeil, der einen Urbildpunkt mit seinem Bildpunkt verbindet, dargestellt werden. Pfeile, die parallel, gleich lang und gleich orientiert sind, beschreiben dieselbe Verschiebung und stellen somit denselben Vektor dar. Zum Beispiel beschreiben im Bild rechts der Pfeil von $A$ nach $A'$, der Pfeil von $B$ nach $B'$ und der Pfeil von $C$ nach $C'$ dieselbe Verschiebung um 7 Einheiten nach rechts und 3 Einheiten nach oben. Sie repräsentieren alle denselben Vektor ${\vec {v}}={\overrightarrow {AA'}}={\overrightarrow {BB'}}={\overrightarrow {CC'}}$. Formal kann man deshalb Vektoren wie folgt definieren:

Ein Pfeil ist eine gerichtete Strecke, das heißt, eine Strecke, bei der eine Reihenfolge der Endpunkte festgelegt ist. Zwei Pfeile heißen äquivalent, wenn sie parallel, gleich lang und gleich gerichtet sind. Dies definiert eine Äquivalenzrelation auf der Menge der Pfeile der Ebene bzw. des Raums. Die Äquivalenzklassen heißen Vektoren.

Eine andere Möglichkeit ist, einen Vektor mit der durch ihn dargestellten Parallelverschiebung zu identifizieren. „Vektor“ ist dann nur eine andere Sprechweise für „Parallelverschiebung“.

Ein Vektor von Startpunkt A nach Endpunkt B und seine Länge

Der Vektor, der eine Verschiebung beschreibt, die den Punkt $A$ auf den Punkt $B$ abbildet, wird als ${\overrightarrow {AB}}$ geschrieben und grafisch durch einen Pfeil dargestellt, der vom Punkt $A$ zum Punkt $B$ zeigt. Man sagt: „Der Vektor ${\vec {a}}={\overrightarrow {AB}}$ bildet $A$ auf $B$ ab“, oder: „Der Vektor ${\vec {a}}={\overrightarrow {AB}}$ verbindet $A$ und $B$.“ Der Punkt $A$ wird in diesem Fall als Schaft, Ausgangs- oder Startpunkt und $B$ als Spitze oder Endpunkt des Vektorpfeils bezeichnet. Der Abstand der beiden Punkte wird Länge oder Betrag des Vektors genannt.

Der umgekehrte Vektor ${\overrightarrow {BA}}$, der $B$ mit $A$ verbindet, heißt Gegenvektor zu ${\overrightarrow {AB}}$. Der Vektor ${\overrightarrow {AA}}$, der einen Punkt $A$ auf sich selbst abbildet, heißt Nullvektor und wird mit ${\vec {0}}$ bezeichnet. Als einziger Vektor kann er grafisch nicht durch einen Pfeil dargestellt werden.

Orts- und Richtungsvektoren

→ Hauptartikel: Ortsvektor

Vektoren können auch dazu verwendet werden, Punkte im Raum zu bezeichnen. So kann der Ort des Punktes $P$ durch den Vektor

${\vec {p}}={\overrightarrow {OP}}$

dargestellt werden. Diesen Vektor nennt man den zum Punkt $P$ gehörenden Ortsvektor. Dabei bezeichnet $O$ den Koordinatenursprung, der für alle Ortsvektoren den Startpunkt bildet.

Um sie davon zu unterscheiden, werden Vektoren, wie sie im vorangegangenen Abschnitt beschrieben wurden, auch als Richtungsvektoren bezeichnet. Zwei Richtungsvektoren sind identisch, wenn sie den gleichen Betrag und die gleiche Richtung haben. Sie können jedoch – wie gezeigt – jeden Punkt des Raums als Startpunkt haben, während Ortsvektoren immer vom Koordinatenursprung ausgehen.

Diese Unterscheidung ist unter anderem in der analytischen Geometrie wichtig. Dort wird beispielsweise eine Gerade durch folgende Gleichung beschrieben:

${\vec {x}}={\vec {p}}+r\cdot {\vec {v}}$

Der Stützvektor ${\vec {p}}$ ist der Ortsvektor eines willkürlich gewählten „Stützpunktes“ der Geraden. Der Richtungsvektor ${\vec {v}}$ gibt die Richtung der Geraden an. Weil $r$ für eine beliebige reelle Zahl steht, ist ${\vec {x}}$ der Ortsvektor eines beliebigen Punktes der Geraden.

Darstellung in Koordinaten

Ein Vektor dargestellt in zwei verschiedenen Basen (lila und rote Pfeile)

Ist, wie in der Abbildung oben, ein geradliniges Koordinatensystem gegeben, so kann ein Vektor der Ebene durch ein geordnetes Zahlenpaar, ein Vektor im Raum durch ein Zahlentripel beschrieben werden. In der Regel werden diese Koordinaten untereinander als sogenannte Spaltenvektoren geschrieben. Für den Vektor in der Ebene, der die Verschiebung um 7 Einheiten nach rechts (in $x$-Richtung) und 3 Einheiten nach oben (in $y$-Richtung) beschreibt, schreibt man ${\vec {v}}={\tbinom {7}{3}}$. Der Vektor ${\tbinom {2}{-5}}$ beschreibt eine Verschiebung um 2 Einheiten in $x$-Richtung und −5 Einheiten in $y$-Richtung, das heißt um 2 Einheiten nach rechts und 5 Einheiten nach unten. Entsprechend beschreibt im Raum der Vektor $\left({\begin{smallmatrix}3\\-2\\4\end{smallmatrix}}\right)$ eine Verschiebung um 3 Einheiten in $x$-Richtung, 2 Einheiten in negativer $y$-Richtung und 4 Einheiten in $z$-Richtung.

Die Komponenten eines Vektors lassen sich als Differenz der Koordinaten von End- und Anfangspunkt berechnen. Im obigen Beispiel haben $A$ und $A'$ die Koordinaten $A(-6|-1)$ und $A'(1|2)$. Die Komponenten des Verbindungsvektors ${\vec {v}}={\overrightarrow {AA'}}$ berechnen sich dann wie folgt:

${\vec {v}}={\overrightarrow {AA'}}={\begin{pmatrix}1-(-6)\\2-(-1)\end{pmatrix}}={\begin{pmatrix}7\\3\end{pmatrix}}$

Beachte, dass die Darstellung eines Vektors durch Tupel von Zahlen bzw. Koordinaten nicht eindeutig ist. So kann der gleiche Vektor durch Basiswechsel in einer anderen Basis gleichwertig durch ein anderes Tupel beschrieben werden.

Betrag, Richtung und Orientierung

Im Gegensatz zu Skalaren haben Vektoren einen Betrag (Länge), eine Richtung und eine Orientierung. Die Richtung ist dabei durch die Achsenlage, die Orientierung durch den Richtungssinn gegeben. Der Richtungssinn gibt dabei an, in welche der beiden Richtungen entlang der Achse der Vektor zeigt. Ein Vorzeichenwechsel in der Größe des Vektors entspricht dabei der Umkehrung des Richtungssinns.

Rechenoperationen

Addition und Subtraktion

Vektoraddition ${\vec {c}}={\vec {a}}+{\vec {b}}$ per Pfeil-Aneinanderreihung

Vektoraddition ${\vec {c}}={\vec {a}}+{\vec {b}}$ per Parallelogramm-Konstruktion

Die Addition von zwei geometrischen Vektoren entspricht der Hintereinanderausführung der zugehörigen Verschiebungen. Stellt der Vektor ${\vec {a}}$ die Verschiebung dar, die den Punkt $P$ auf $Q$ abbildet, und bildet die zu ${\vec {b}}$ gehörige Verschiebung den Punkt $Q$ auf $R$ ab, so beschreibt ${\vec {a}}+{\vec {b}}$ die Verschiebung, die $P$ auf $R$ abbildet:

${\overrightarrow {PQ}}+{\overrightarrow {QR}}={\overrightarrow {PR}}$

Geometrisch kann man deshalb zwei Vektoren ${\vec {a}}$ und ${\vec {b}}$ addieren, indem man die beiden Vektoren so durch Pfeile darstellt, dass der Startpunkt des zweiten mit dem Endpunkt des ersten Pfeils übereinstimmt. Die Summe ${\vec {c}}={\vec {a}}+{\vec {b}}$ wird dann durch den Pfeil vom Startpunkt des ersten bis zum Endpunkt des zweiten Pfeils dargestellt.

Alternativ stellt man die beiden Vektoren durch Pfeile mit einem gemeinsamen Anfangspunkt dar und ergänzt diese Figur zu einem Parallelogramm. Der diagonale Pfeil vom gemeinsamen Anfangspunkt zur gegenüberliegenden Ecke stellt dann die Summe der beiden Vektoren dar. In der Physik verwendet man diese Konstruktion beim Kräfteparallelogramm.

In Koordinaten berechnet man die Summe komponentenweise: Für die Summe der beiden Vektoren

${\vec {a}}={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}$ und ${\vec {b}}={\begin{pmatrix}b_{1}\\b_{2}\\b_{3}\end{pmatrix}}$

gilt

${\vec {a}}+{\vec {b}}={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}+{\begin{pmatrix}b_{1}\\b_{2}\\b_{3}\end{pmatrix}}={\begin{pmatrix}a_{1}+b_{1}\\a_{2}+b_{2}\\a_{3}+b_{3}\end{pmatrix}}$.

Für die Addition von Vektoren gelten das Assoziativ- und das Kommutativgesetz.

Vektorsubtraktion ${\vec {c}}={\vec {a}}-{\vec {b}}={\vec {a}}+(-{\vec {b}})$ per Pfeil-Aneinanderreihung mit Gegenvektor

Vektorsubtraktion ${\vec {c}}={\vec {a}}-{\vec {b}}$ per Konstruktion mit Pfeilen mit demselben Anfangspunkt

Für die Differenz zweier Vektoren ${\vec {a}}$ und ${\vec {b}}$ gilt

${\vec {a}}-{\vec {b}}={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}-{\begin{pmatrix}b_{1}\\b_{2}\\b_{3}\end{pmatrix}}={\begin{pmatrix}a_{1}-b_{1}\\a_{2}-b_{2}\\a_{3}-b_{3}\end{pmatrix}}$.

Sie lässt sich auf zwei Arten geometrisch deuten:

• Als die Summe von ${\vec {a}}$ mit dem Gegenvektor $-{\vec {b}}$ von ${\vec {b}}$. Man setzt den Startpunkt eines Pfeils, der den Gegenvektor von ${\vec {b}}$ darstellt, an den Endpunkt des Pfeils, der ${\vec {a}}$ darstellt.
• Als denjenigen Vektor, der zu ${\vec {b}}$ addiert gerade ${\vec {a}}$ ergibt. Stellt man ${\vec {a}}$ und ${\vec {b}}$ durch Pfeile mit demselben Anfangspunkt dar, so wird ${\vec {a}}-{\vec {b}}$ durch den Pfeil dargestellt, der vom Endpunkt des zweiten Vektors zum Endpunkt des ersten Vektors führt.

Werden zwei Vektoren addiert (subtrahiert), so addieren (subtrahieren) sich ihre Beträge nur dann, wenn die Vektoren kollinear sind und die gleiche Orientierung haben. Im allgemeinen Fall gilt hingegen die Dreiecksungleichung

$\left|{\vec {a}}+{\vec {b}}\right|\leq \left|{\vec {a}}\right|+\left|{\vec {b}}\right|$.

Multiplikation mit einem Skalar

Skalarmultiplikation

Vektoren können mit reellen Zahlen (oft Skalare genannt, um sie von Vektoren zu unterscheiden) multipliziert werden (Skalarmultiplikation, auch S-Multiplikation genannt):

$r{\vec {a}}=r\,{\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}={\begin{pmatrix}ra_{1}\\ra_{2}\\ra_{3}\end{pmatrix}}$

Die Länge des resultierenden Vektors ist $|r|\cdot |{\vec {a}}|$. Wenn der Skalar positiv ist, zeigt der resultierende Vektor in dieselbe Richtung wie der ursprüngliche, ist er negativ, in die Gegenrichtung.

Für die Vektoraddition und die Multiplikation mit einem Skalar gilt das Distributivgesetz:

$r\cdot ({\vec {a}}+{\vec {b}})=r{\vec {a}}+r{\vec {b}}$

Ebenso gilt es für die Addition von zwei Skalaren:

$(r+s)\cdot {\vec {a}}=r{\vec {a}}+s{\vec {a}}$

Skalarprodukt

→ Hauptartikel: Skalarprodukt

Das Skalarprodukt zweier Vektoren hängt von der Länge der Vektoren und dem eingeschlossenen Winkel ab

Das Skalarprodukt (oder innere Produkt) zweier Vektoren ${\vec {a}}$ und ${\vec {b}}$, so genannt, weil das Ergebnis ein Skalar ist, wird als ${\vec {a}}\cdot {\vec {b}},\ {\vec {a}}\circ {\vec {b}},\ {\vec {a}}\bullet {\vec {b}}$ oder $\langle {{\vec {a}},{\vec {b}}}\rangle$ notiert und ist definiert als

${\vec {a}}\cdot {\vec {b}}=|{\vec {a}}|\,|{\vec {b}}|\,\cos \varphi ,$

wobei $\varphi$ der zwischen den beiden Vektoren eingeschlossene Winkel ist (siehe auch Kosinus). Stehen die zwei Vektoren rechtwinklig aufeinander, so ist ${\vec {a}}\cdot {\vec {b}}=0$, da $\cos 90^{\circ }=0$ gilt.

Im kartesischen Koordinatensystem berechnet sich das Skalarprodukt zu

${\vec {a}}\cdot {\vec {b}}={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}\cdot {\begin{pmatrix}b_{1}\\b_{2}\\b_{3}\end{pmatrix}}=a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}$,

Orthogonale Projektion ${\vec {b}}_{\vec {a}}$ des Vektors ${\vec {b}}$ auf die durch ${\vec {a}}$ bestimmte Richtung

Geometrisch lässt sich das Skalarprodukt auch wie folgt verstehen (s. Abbildung): Man projiziert den einen Vektor ${\vec {b}}$ senkrecht auf den anderen ${\vec {a}}$ und erhält so den Vektor ${\vec {b}}_{\vec {a}}$. Falls der von den beiden Vektoren eingeschlossene Winkel $\varphi$ ein spitzer Winkel ist, zeigt ${\vec {b}}_{\vec {a}}$ in dieselbe Richtung wie ${\vec {a}}$. In diesem Falle ergibt sich das Skalarprodukt durch die Multiplikation der beiden Beträge von ${\vec {a}}$ und ${\vec {b}}_{\vec {a}}$. Diese Zahl ist positiv. Handelt es sich hingegen um einen stumpfen Winkel, so ist die Projektion antiparallel zu ${\vec {a}}$ und das Skalarprodukt hat daher ein negatives Vorzeichen. Wenn die beiden Vektoren einen rechten Winkel einschließen ($\varphi =90^{\circ }$), dann ist die Länge des projizierten Vektors null und damit auch das Skalarprodukt. (Vertauscht man die beiden Vektoren bei diesem Vorgehen, so ergibt sich derselbe Wert.)

Diese Operation wird oft in der Physik gebraucht, zum Beispiel, um die Arbeit zu berechnen, wenn die Richtung der Kraft nicht mit der Bewegungsrichtung übereinstimmt.

Für das Skalarprodukt gelten das Kommutativgesetz

${\vec {a}}\cdot {\vec {b}}={\vec {b}}\cdot {\vec {a}}$

und das Distributivgesetz

${\vec {a}}\cdot ({\vec {b}}+{\vec {c}})={\vec {a}}\cdot {\vec {b}}+{\vec {a}}\cdot {\vec {c}}.$

Kreuzprodukt

→ Hauptartikel: Kreuzprodukt

Veranschaulichung des Kreuzprodukts

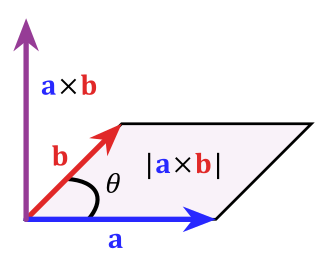
Das Kreuzprodukt (auch vektorielles Produkt, äußeres Produkt oder Vektorprodukt) ${\vec {a}}\times {\vec {b}}$ (gesprochen als „a Kreuz b“) zweier Vektoren im dreidimensionalen euklidischen Vektorraum ist ein bestimmter Vektor, der senkrecht auf der von ${\vec {a}}$ und ${\vec {b}}$ aufgespannten Ebene steht. Die Länge $|{\vec {a}}\times {\vec {b}}|$ dieses Vektors ist gleich der Fläche des Parallelogramms mit den Seiten ${\vec {a}}$ und ${\vec {b}}$, also

$|{\vec {a}}\times {\vec {b}}|=|{\vec {a}}|\cdot |{\vec {b}}|\cdot {\mathopen {|}}\sin \theta {\mathclose {|}}$,

wobei der von den beiden Vektoren eingeschlossene Winkel hier mit $\theta$ bezeichnet wird. Das Kreuzprodukt zweier kollinearer Vektoren ergibt daher den Nullvektor.

Im dreidimensionalen kartesischen Koordinatensystem lässt sich das Kreuzprodukt wie folgt berechnen:

${\vec {a}}\times {\vec {b}}={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}\times {\begin{pmatrix}b_{1}\\b_{2}\\b_{3}\end{pmatrix}}={\begin{pmatrix}a_{2}b_{3}-a_{3}b_{2}\\a_{3}b_{1}-a_{1}b_{3}\\a_{1}b_{2}-a_{2}b_{1}\end{pmatrix}}$

Das Kreuzprodukt ist antikommutativ, d. h., es gilt

${\vec {a}}\times {\vec {b}}=-({\vec {b}}\times {\vec {a}})$.

Spatprodukt

→ Hauptartikel: Spatprodukt

Die Kombination von Kreuz- und Skalarprodukt in der Form

$({\vec {a}},{\vec {b}},{\vec {c}})=({\vec {a}}\times {\vec {b}})\cdot {\vec {c}}$

wird als Spatprodukt bezeichnet. Das Ergebnis ist ein Skalar. Sein Betrag ist das Volumen des Spats, der von den drei Vektoren aufgespannt wird. Bilden die drei Vektoren ein Rechtssystem, so ist $({\vec {a}},{\vec {b}},{\vec {c}})$ positiv. Bilden sie ein Linkssystem, so ist $({\vec {a}},{\vec {b}},{\vec {c}})$ negativ. Wenn die Vektoren linear abhängig sind, gilt $({\vec {a}},{\vec {b}},{\vec {c}})=0$.

Länge/Betrag eines Vektors

In kartesischen Koordinaten kann die Länge von Vektoren nach dem Satz des Pythagoras berechnet werden:

$a=|{\vec {a}}|={\sqrt {{a_{1}}^{2}+{a_{2}}^{2}+{a_{3}}^{2}}}$

Dies entspricht der euklidischen Norm. Die Länge lässt sich in einer alternativen Schreibweise auch als die Wurzel des Skalarprodukts angeben:

$a=|{\vec {a}}|={\sqrt {{\vec {a}}\cdot {\vec {a}}}}$

Vektoren der Länge 1 heißen Einheitsvektoren. Hat ein Vektor die Länge 0, so handelt es sich um den Nullvektor.

Bei vektoriellen Größen in der Physik spricht man statt von der Länge vom Betrag eines Vektors. Man kann eine vektorielle physikalische Größe ${\vec {v}}$ als Paar $({\vec {e}}_{v},|{\vec {v}}|)$ aus Richtung der Größe als Einheitsvektor ${\vec {e}}_{v}$ und Betrag der Größe entlang dieser Richtung ansehen. Die Einheit des Betrags ist dabei gleich der Einheit der physikalischen Größe. So lässt sich beispielsweise die Geschwindigkeit

${\vec {v}}={\begin{pmatrix}3\\-4\\0\end{pmatrix}}\,\mathrm {\frac {m}{s}}$

eines Hubschraubers, der in konstanter Höhe in südöstlicher Richtung fliegt, durch

${\vec {e}}_{v}={\frac {1}{|{\vec {v}}|}}{\vec {v}}={\begin{pmatrix}{\tfrac {3}{5}}\\-{\tfrac {4}{5}}\\0\end{pmatrix}}$

und

$|{\vec {v}}|={\sqrt {3^{2}+(-4)^{2}+0^{2}}}\,\mathrm {\frac {m}{s}} =5\,\mathrm {\frac {m}{s}}$

darstellen. Der Betrag der Bahngeschwindigkeit $v(t)$ beim waagrechten Wurf (Startgeschwindigkeit in $x$-Richtung $v_{x}$, aktuelle Geschwindigkeit in $y$-Richtung $v_{y}(t)$) lässt sich angeben als

$v(t)={|{\vec {v}}(t)|}={\sqrt {v_{x}^{2}+v_{y}^{2}}}$.

Dyadisches Produkt

→ Hauptartikel: Dyadisches Produkt

Abbildung eines Vektors ${\vec {c}}$ auf den Vektor ${\vec {d}}=({\vec {a}}\otimes {\vec {b}})\cdot {\vec {c}}$

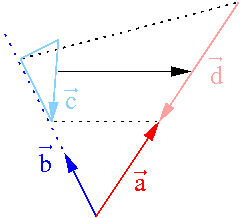
Das dyadische oder tensorielle Produkt ${\vec {a}}\otimes {\vec {b}}$ oder ${\vec {a}}{\vec {b}}$ (gesprochen als „a dyadisch b“) zweier Vektoren bildet eine Dyade. Mit Dyaden kann ein Vektor linear auf einen anderen Vektor abgebildet werden, siehe Bild. Der Anteil eines Vektors ${\vec {c}}$ in Richtung des Vektors ${\vec {b}}$ wird dabei in die Richtung des Vektors ${\vec {a}}$ gebracht und dabei gestreckt oder gestaucht. Die Abbildung geschieht mit dem obigen Skalarprodukt:

$({\vec {a}}\otimes {\vec {b}})\cdot {\vec {c}}:=({\vec {b}}\cdot {\vec {c}}){\vec {a}}$

Im dreidimensionalen kartesischen Koordinatensystem lässt sich das dyadische Produkt wie folgt berechnen:

${\vec {a}}\otimes {\vec {b}}={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}\otimes {\begin{pmatrix}b_{1}\\b_{2}\\b_{3}\end{pmatrix}}={\begin{pmatrix}a_{1}b_{1}&a_{1}b_{2}&a_{1}b_{3}\\a_{2}b_{1}&a_{2}b_{2}&a_{2}b_{3}\\a_{3}b_{1}&a_{3}b_{2}&a_{3}b_{3}\end{pmatrix}}$

Das dyadische Produkt ist nicht kommutativ, d. h., im Allgemeinen gilt

${\vec {a}}\otimes {\vec {b}}\neq {\vec {b}}\otimes {\vec {a}}$,

aber distributiv mit der Vektoraddition:

${\begin{aligned}({\vec {a}}+{\vec {b}})\otimes {\vec {c}}={\vec {a}}\otimes {\vec {c}}+{\vec {b}}\otimes {\vec {c}}\\{\vec {a}}\otimes ({\vec {b}}+{\vec {c}})={\vec {a}}\otimes {\vec {b}}+{\vec {a}}\otimes {\vec {c}}\end{aligned}}$

Es ist auch verträglich mit der Skalarmultiplikation:

$\lambda ({\vec {a}}\otimes {\vec {b}})=(\lambda {\vec {a}})\otimes {\vec {b}}={\vec {a}}\otimes (\lambda {\vec {b}})=\lambda {\vec {a}}\otimes {\vec {b}}$

Durch das dyadische Produkt entsteht eine neue Klasse von Objekten der linearen Algebra, die Matrizen und linearen Abbildungen, je nachdem, ob im Koordinatenraum oder Vektorraum gerechnet wird. Durch Verknüpfung mehrerer Dyaden (wie in ${\vec {a}}\otimes {\vec {b}}\otimes {\vec {c}}\dotsm$) entstehen Dyaden höherer Stufe. Dyaden bilden einen Spezialfall von Tensoren. Tensoren spielen in der Kontinuumsmechanik, den Maxwell-Gleichungen des Elektromagnetismus und der allgemeinen Relativitätstheorie eine wichtige Rolle. Einen Überblick über die Tensoralgebra gibt die Formelsammlung Tensoralgebra.

Komponentenschreibweise

Alternativ zu der hier vorgestellten Schreibweise als Spaltenvektoren können Vektoren auch in Komponentenschreibweise dargestellt werden. Dabei steht $a_{i}$ üblicherweise für die einzelnen Komponenten des Vektors ${\vec {a}}$ bezüglich der Standardbasis. Dadurch lassen sich die Rechenoperationen bezüglich der Standardbasis wie folgt schreiben:

	Spaltenvektoren	Komponentenschreibweise
Addition/Subtraktion	${\vec {c}}={\vec {a}}\pm {\vec {b}}={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}\pm {\begin{pmatrix}b_{1}\\b_{2}\\b_{3}\end{pmatrix}}={\begin{pmatrix}a_{1}\pm b_{1}\\a_{2}\pm b_{2}\\a_{3}\pm b_{3}\end{pmatrix}}$	$c_{i}=a_{i}\pm b_{i}$
Skalarprodukt	$c={\vec {a}}\cdot {\vec {b}}={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}\cdot {\begin{pmatrix}b_{1}\\b_{2}\\b_{3}\end{pmatrix}}=a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}$	$c=\sum _{i}a_{i}b_{i}$ beziehungsweise: $c=a_{i}b_{i}$
Betrag	$a=|{\vec {a}}|={\sqrt {{a_{1}}^{2}+{a_{2}}^{2}+{a_{3}}^{2}}}$	$a={\sqrt {\sum _{i}a_{i}^{2}}}$ beziehungsweise: $a={\sqrt {a_{i}a_{i}}}$
Kreuzprodukt	${\vec {c}}={\vec {a}}\times {\vec {b}}={\begin{pmatrix}a_{1}\\a_{2}\\a_{3}\end{pmatrix}}\times {\begin{pmatrix}b_{1}\\b_{2}\\b_{3}\end{pmatrix}}={\begin{pmatrix}a_{2}b_{3}-a_{3}b_{2}\\a_{3}b_{1}-a_{1}b_{3}\\a_{1}b_{2}-a_{2}b_{1}\end{pmatrix}}$	$c_{i}=\sum _{jk}\varepsilon _{ijk}a_{j}b_{k}$ beziehungsweise: $c_{i}=\varepsilon _{ijk}a_{j}b_{k}$

Siehe auch den Abschnitt Koordinaten und Komponenten eines Vektors unten.

n-Tupel und Spaltenvektoren

In Verallgemeinerung der Koordinatendarstellung von geometrischen Vektoren werden Elemente von $\mathbb {R} ^{n}$, also $n$-Tupel reeller Zahlen, als Vektoren bezeichnet, wenn mit ihnen die für Vektoren typischen Rechenoperationen Addition und skalare Multiplikation ausgeführt werden. In der Regel werden die $n$-Tupel als sogenannte Spaltenvektoren geschrieben, das heißt, ihre Einträge stehen untereinander.

Addition und skalare Multiplikation

Die Addition zweier Vektoren ${\vec {x}},{\vec {y}}\in \mathbb {R} ^{n}$ und die skalare Multiplikation eines Vektors mit einer Zahl $r\in \mathbb {R}$ werden komponentenweise definiert:

${\vec {x}}+{\vec {y}}={\begin{pmatrix}x_{1}\\\vdots \\x_{n}\end{pmatrix}}+{\begin{pmatrix}y_{1}\\\vdots \\y_{n}\end{pmatrix}}:={\begin{pmatrix}x_{1}+y_{1}\\\vdots \\x_{n}+y_{n}\end{pmatrix}},\quad r{\vec {x}}=r{\begin{pmatrix}x_{1}\\\vdots \\x_{n}\end{pmatrix}}:={\begin{pmatrix}rx_{1}\\\vdots \\rx_{n}\end{pmatrix}}$

Die Menge $\mathbb {R} ^{n}$ bildet mit diesen Verknüpfungen einen Vektorraum über dem Körper $\mathbb {R}$. Dieser sogenannte Koordinatenraum ist das Standardbeispiel eines $n$-dimensionalen $\mathbb {R}$-Vektorraums.

Standardskalarprodukt

→ Hauptartikel: Standardskalarprodukt

Das Standardskalarprodukt ist definiert durch

${\vec {x}}\cdot {\vec {y}}={\begin{pmatrix}x_{1}\\\vdots \\x_{n}\end{pmatrix}}\cdot {\begin{pmatrix}y_{1}\\\vdots \\y_{n}\end{pmatrix}}:=x_{1}y_{1}+\dotsb +x_{n}y_{n}$.

Mit diesem Skalarprodukt ist der $\mathbb {R} ^{n}$ ein euklidischer Vektorraum.

Multiplikation mit einer Matrix

→ Hauptartikel: Matrix-Vektor-Produkt

Ist $A\in \mathbb {R} ^{m\times n}$ eine ($m\times n$)-Matrix und ${\vec {x}}\in \mathbb {R} ^{n}$ ein Spaltenvektor, so kann man ${\vec {x}}$ als einspaltige Matrix in $\mathbb {R} ^{n\times 1}$ auffassen und das Matrix-Vektor-Produkt $A{\vec {x}}$ bilden. Das Ergebnis ist ein Spaltenvektor in $\mathbb {R} ^{m}$:

$A{\vec {x}}={\begin{pmatrix}a_{11}&\dots &a_{1n}\\\vdots &\ddots &\vdots \\a_{m1}&\dots &a_{mn}\end{pmatrix}}\,{\begin{pmatrix}x_{1}\\\vdots \\x_{n}\end{pmatrix}}={\begin{pmatrix}a_{11}x_{1}+\dotsb +a_{1n}x_{n}\\\vdots \\a_{m1}x_{1}+\dotsb +a_{mn}x_{n}\end{pmatrix}}$

Die Multiplikation mit einer ($m\times n$)-Matrix ist eine lineare Abbildung von $\mathbb {R} ^{n}$ nach $\mathbb {R} ^{m}$. Jede lineare Abbildung lässt sich als Multiplikation mit einer Matrix darstellen.

Länge bzw. Norm

→ Hauptartikel: Euklidische Norm

Die Länge oder Norm eines Vektors ist durch die Quadratwurzel aus dem Skalarprodukt mit sich selbst gegeben:

$|{\vec {x}}|={\sqrt {{\vec {x}}\cdot {\vec {x}}}}={\sqrt {x_{1}^{2}+\dotsb +x_{n}^{2}}}$

Neben dieser euklidischen Norm werden auch andere Normen benutzt, siehe p-Norm.

Zeilen- und Spaltenvektoren

Fasst man Vektoren als Matrizen auf, so ist eine $n\times 1$-Matrix ein Spaltenvektor

${\vec {x}}={\begin{pmatrix}x_{1}\\\vdots \\x_{n}\end{pmatrix}}$,

zu dem es eine $1\times n$-Matrix

${\vec {x}}^{\top }=(x_{1}\ \dotsc \ x_{n})$

als zugehörigen Zeilenvektor gibt, wobei ${\vec {x}}^{\top }$ die Transponierte von ${\vec {x}}$ ist. In dieser Schreibweise ist das Standardskalarprodukt nichts anderes als das Matrixprodukt einer $1\times n$-Matrix mit einer $n\times 1$-Matrix:

${\vec {x}}\cdot {\vec {y}}={\vec {x}}^{\top }{\vec {y}}=(x_{1}\ \dotsc \ x_{n})\ {\begin{pmatrix}y_{1}\\\vdots \\y_{n}\end{pmatrix}}=x_{1}y_{1}+\dotsb +x_{n}y_{n}$

Das dyadische Produkt stellt sich als das Matrixprodukt einer $n\times 1$-Matrix mit einer $1\times n$-Matrix dar und liefert dann eine $n\times n$-Matrix:

${\vec {x}}\otimes {\vec {y}}={\vec {x}}\,{\vec {y}}^{\top }={\begin{pmatrix}x_{1}\\\vdots \\x_{n}\end{pmatrix}}\ (y_{1}\ \dotsc \ y_{n})={\begin{pmatrix}x_{1}y_{1}&\ldots &x_{1}y_{n}\\\vdots &\ddots &\vdots \\x_{n}y_{1}&\ldots &x_{n}y_{n}\end{pmatrix}}$

Eigenschaften von Vektoren

Lineare Abhängigkeit

→ Hauptartikel: Lineare Unabhängigkeit

Vektoren ${\vec {a}}_{1},{\vec {a}}_{2},\dotsc ,{\vec {a}}_{m}$ ($m\in \mathbb {N}$) heißen linear abhängig, wenn es für die folgende Gleichung eine Lösung gibt, bei der nicht für alle Koeffizienten $r_{i}=0$ gilt:

$r_{1}\cdot {\vec {a}}_{1}+r_{2}\cdot {\vec {a}}_{2}+\dotsb +r_{m}\cdot {\vec {a}}_{m}={\vec {0}}{\text{ mit }}r_{i}\in \mathbb {R}$

Wenn sich jedoch keine Koeffizienten $r_{i}$ finden lassen, die diese Bedingung erfüllen, dann nennt man die Vektoren linear unabhängig.

Im Fall der linearen Abhängigkeit lässt sich mindestens einer der Vektoren als eine Linearkombination der anderen darstellen. Umgekehrt gilt: Falls sich einer der Vektoren als Linearkombination der anderen darstellen lässt, sind die gegebenen Vektoren linear abhängig.

Um ein Koordinatensystem für einen $n$-dimensionalen Raum festzulegen, braucht man genau $n$ linear unabhängige Basisvektoren. Dann kann man jeden Vektor dieses Raums auf eindeutige Weise als Linearkombination der Basisvektoren schreiben. Mehr als $n$ Vektoren im $n$-dimensionalen Raum sind stets linear abhängig.

Kollinearität zweier Vektoren

Zwei linear abhängige Vektoren ${\vec {a}}$ und ${\vec {b}}$ nennt man auch kollinear. Im dreidimensionalen Raum gilt für sie

${\vec {a}}\times {\vec {b}}={\vec {0}}.$

Jeder Vektor ist mit dem Nullvektor kollinear. Handelt es sich aber um zwei vom Nullvektor verschiedene Vektoren, so sind sie genau dann kollinear, wenn

${\vec {a}}=r\cdot {\vec {b}}$

für ein $r\neq 0$ erfüllt ist. Sie sind parallel, wenn $r$ positiv, und antiparallel, wenn $r$ negativ ist.

Orthogonalität

Zwei Vektoren ${\vec {a}}$ und ${\vec {b}}$ sind orthogonal, wenn ihr Skalarprodukt gleich 0 ist:

${\vec {a}}\cdot {\vec {b}}=0$

Bei geometrischen Vektoren mit positiver Länge bedeutet dies, dass sie einen rechten Winkel einschließen, siehe Skalarprodukt. Der Nullvektor ist zu jedem Vektor orthogonal.

Normierung

Ein Vektor ${\hat {a}}$ (gelesen „a Dach“) heißt Einheitsvektor oder normiert, wenn er die Länge 1 hat. Man normiert einen Vektor ${\vec {a}}\neq {\vec {0}}$, indem man ihn durch seine Länge dividiert, d. h., mit dem Kehrwert seiner Länge multipliziert:

${\hat {a}}={\frac {\vec {a}}{|{\vec {a}}|}}$

Der Vektor ${\hat {a}}$ hat dieselbe Richtung wie ${\vec {a}}$, aber die Länge 1. Andere Schreibweisen für ${\hat {a}}$ sind ${\vec {e}}_{a}$, ${\vec {a}}_{0}$ oder ${\vec {a}}{}^{\circ }$.

Einheitsvektoren sind bei der Darstellung von Koordinatensystemen von Bedeutung.

Koordinaten und Komponenten eines Vektors

Vektor (schwarz) mit Komponenten (rot) und Koordinaten (grün) bezüglich eines Koordinatensystems (grau)

→ Hauptartikel: Vektorraumbasis

Das am weitesten verbreitete Koordinatensystem, das kartesische, ist z. B. ein Orthonormalsystem, weil es von den drei zueinander orthogonalen Einheitsvektoren ${\hat {e}}_{1}$, ${\hat {e}}_{2}$ und ${\hat {e}}_{3}$ der Standardbasis aufgespannt wird. Die Koordinaten eines Vektors sind dann die Skalarprodukte des Vektors mit den Basisvektoren:

$a_{i}={\vec {a}}\cdot {\hat {e}}_{i}$

So kann jeder Vektor als Linearkombination der Basisvektoren dargestellt werden, indem man ihn als Summe seiner Komponenten bezüglich der Basis schreibt:

${\vec {a}}=\sum _{i=1}^{3}\left({\vec {a}}\cdot {\hat {e}}_{i}\right){\hat {e}}_{i}=\left({\vec {a}}\cdot {\hat {e}}_{1}\right){\hat {e}}_{1}+\left({\vec {a}}\cdot {\hat {e}}_{2}\right){\hat {e}}_{2}+\left({\vec {a}}\cdot {\hat {e}}_{3}\right){\hat {e}}_{3}$

Durch einen Wechsel zu einer anderen Orthonormalbasis $\{{\hat {g}}_{1},{\hat {g}}_{2},{\hat {g}}_{3}\}$ bekommt der Vektor andere Koordinaten $a_{i}^{\prime }={\vec {a}}\cdot {\hat {g}}_{i}$ und andere Komponenten:

${\vec {a}}=\sum _{i=1}^{3}\left({\vec {a}}\cdot {\hat {g}}_{i}\right){\hat {g}}_{i}=\left({\vec {a}}\cdot {\hat {g}}_{1}\right){\hat {g}}_{1}+\left({\vec {a}}\cdot {\hat {g}}_{2}\right){\hat {g}}_{2}+\left({\vec {a}}\cdot {\hat {g}}_{3}\right){\hat {g}}_{3}$

Allgemeiner können drei beliebige, aber linear unabhängige Vektoren als Vektorraumbasis benutzt werden.

Verallgemeinerungen

Die Definition des Vektors in der linearen Algebra als Element eines Vektorraumes ist eine viel umfassendere, die neben den herkömmlichen, geometrischen Vektoren verschiedenste mathematische Objekte (Zahlen, Folgen, Funktionen und Transformationen) beinhaltet.

Andererseits sind Vektoren gerade einstufige Tensoren, d. h. Tensoren mit nur einem Index.

Vektoren in der Physik

→ Hauptartikel: Vektorielle Größe

Vektorgrößen im euklidischen Raum unserer Anschauung

In der klassischen Physik werden physikalische Größen, die einen Betrag und eine Richtung haben, als Vektoren des euklidischen Raums aufgefasst. Beispiele hierfür sind der Ort, die Geschwindigkeit, die Beschleunigung, die Kraft usw. Man kann sie skalaren physikalischen Größen gegenüberstellen, die nur einen Betrag, jedoch keine Richtung haben, wie z. B. Volumen, Masse, Ladung, Temperatur usw.

Diese Auffassung gerichteter physikalischer Größen als Vektoren ist eine Anwendung geometrischer Vektoren. An die Stelle der Verschieberichtung tritt die Richtung der physikalischen Größe. Ihr Betrag entspricht der Verschiebungsweite eines geometrischen Vektors. Die Darstellung solcher Größen durch Pfeile bestimmter Länge veranschaulicht sowohl deren Richtung als auch deren Betrag. Folglich gilt alles, was bereits über geometrische Vektoren gesagt wurde, auch für vektorielle Größen in der Physik, insbesondere auch das über Rechenoperationen und graphische Veranschaulichung Gesagte.

Physikalische Größen lassen sich nur dann addieren, wenn es sich um Größen derselben Größenart handelt. Das gilt auch dann, wenn man sie als Vektoren auffasst. Die Addition wird z. B. durch das Kräfteparallelogramm veranschaulicht. Vektorsummen sind unter anderem in der Statik von herausragender Bedeutung, z. B. bei der Definition des Kräftegleichgewichts $\sum {\vec {F}}_{i}=0$.

Das Skalarprodukt wird verwendet, wenn die Projektion eines Vektors in die Richtung eines anderen von Bedeutung ist. Beispielsweise versteht man unter dem physikalischen Begriff Arbeit das Produkt einer Kraft und eines Weges in Kraftrichtung. Deswegen berechnet man die Arbeit über das Skalarprodukt der Kraft und des Weges. Außerdem ist das Skalarprodukt wichtig bei der Komponentenzerlegung eines Vektors. Das Kreuzprodukt hingegen findet überall dort Verwendung, wo eine Gesetzmäßigkeit der Drei-Finger-Regel folgt, wie z. B. bei der Lorentzkraft oder dem Drehmoment. Sowohl beim Skalarprodukt als auch beim Kreuzprodukt ergibt sich die Einheit der resultierenden physikalischen Größe durch die Multiplikation der Einheiten beider Faktoren.

Ist ein physikalischer Vektor selbst eine Funktion des Ortes, spricht man von einem Vektorfeld. Es kann durch Feldlinien veranschaulicht werden, wobei die Tangente an die Feldlinie die Richtung des Vektors angibt. Der Betrag des Vektors wird durch die Dichte der Feldlinien dargestellt. Als Beispiele wären hier vor allem die elektrischen und magnetischen Felder sowie die Geschwindigkeitsfelder in Strömungen zu nennen. Bei der mathematischen Behandlung der Felder erweist sich die Vektoranalysis als äußerst wichtiges Werkzeug, z. B. in der Elektrodynamik oder in der Strömungsmechanik.

Vektoren in nicht-euklidischen Räumen der relativistischen Physik

An die Stelle des dreidimensionalen euklidischen Raums tritt in der Relativitätstheorie die nichteuklidische vierdimensionale Raumzeit. Vektorielle Größen wie die Vierergeschwindigkeit oder der Viererimpuls werden hier dementsprechend als vierdimensionale Vektoren dargestellt.

Transformationsverhalten von Vektoren

In der Physik werden Vektoren (auch) durch ihr Transformationsverhalten beim Wechsel von Bezugssystemen charakterisiert.

Polare und axiale Vektoren

Je nach Transformationsverhalten unter Punktspiegelungen des Ortes unterscheidet man zwischen polaren und axialen Vektoren, in der älteren Literatur auch Schub- und Drehvektoren genannt: In euklidischen Vektorräumen geht jeder Vektor bei der räumlichen Punktspiegelung in sein Negatives über, Axialvektoren dagegen bleiben dabei unverändert. So ändern beispielsweise der Ort, die Geschwindigkeit, der Impuls und das elektrische Feld bei räumlicher Punktspiegelung ihr Vorzeichen, nicht aber der Drehimpuls oder das magnetische Feld. Polare und axiale Vektoren sind wegen ihres unterschiedlichen Transformationsverhaltens Elemente verschiedener Vektorräume. Das Kreuzprodukt muss dabei als bilineare Abbildung zweier Vektorräume in einen dritten angesehen werden.

Diese Sichtweise in der Physik ist davon abhängig, ob man in einem euklidischen oder nicht-euklidischen Raum arbeitet.

Transformationsverhalten im euklidischen- und Minkowski-Raum

Für den physikalischen Vektorbegriff ist das Transformationsverhalten unter der Isometriegruppe der entsprechenden Metrik des zugrunde gelegten Raumes von Bedeutung. Der dreidimensionale Raum der klassischen Mechanik wird als euklidischer flacher Raum modelliert, während die vierdimensionale Raumzeit der Relativitätstheorie als Minkowski-Raum mit einer gekrümmten Metrik versehen wird. Diese Räume sind Mannigfaltigkeiten, in denen Vektoren kontravariante Tensoren erster Stufe darstellen, was ihr Transformationsverhalten festlegt. Die Isometriegruppen sind im euklidischen Raum die Drehgruppe und im Minkowski-Raum die Lorentz-Gruppe.

Nicht alle Vektoren im Dreidimensionalen sind Teile von Vierervektoren. Der Drehimpuls transformiert beispielsweise unter Lorentztransformationen nicht wie ein Teil eines Vierervektors, sondern zusammen mit dem anfänglichen Energieschwerpunkt wie die sechs Komponenten eines antisymmetrischen Tensors. Ebenso transformieren die elektrische und magnetische Feldstärke wie die sechs Komponenten eines antisymmetrischen Tensors.

Vielteilchensysteme mit $n$ Teilchen beschreibt man mit Vektoren in $3n$-dimensionalen Vektorräumen, auf die die dreidimensionale Drehgruppe getrennt wirkt.

Weitere Verwendungen des Vektorbegriffs in der Physik

Mehrteilchen-Systeme von $n$ Teilchen beschreibt man durch Vektoren in $3n$-dimensionalen Vektorräumen, bzw. – in der hamiltonschen Mechanik – im $6n$-dimensionalen Phasenraum, der nicht nur die Ortskoordinaten, sondern auch die Impulskoordinaten umfasst. Schließlich werden die Zustände quantenmechanischer Systeme als Vektoren in Funktionenräumen dargestellt. Hier erweist sich insbesondere die Bra-Ket-Notation, die von Paul Dirac eingeführt wurde, als hilfreich.

Literatur

• Kurt Bohner, Peter Ihlenburg, Roland Ott: Mathematik für berufliche Gymnasien – Lineare Algebra – Vektorgeometrie. Merkur, Rinteln 2016, ISBN 978-3-8120-0638-5.
• Klaus Jänich: Lineare Algebra. 11. Auflage. Springer, Berlin 2013, ISBN 978-3-540-75501-2.
• Lothar Papula: Mathematik für Ingenieure und Naturwissenschaftler. Band 1. 15. Auflage, Springer Vieweg, Wiesbaden 2018, ISBN 978-3-658-21745-7.

Weblinks

Wiktionary: Vektor – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Commons: Vektoren – Sammlung von Bildern, Videos und Audiodateien

• Ronny Harbich: Vektorrechnung fürs Abitur. Bei: fabulierer.de.
• Vektoren. Bei: mathe-online.at.
• History of Vectors. Bei: math.mcgill.ca.