Mohó algoritmus

Mohó algoritmussal gyorsan meghatározható a legkevesebb pénzérme, amivel ki lehet az aprót fizetni. A legnagyobb értékű érme, amivel ki lehet fizetni a megmaradt összeget, a helyi optimum.

Gyengeség 1.: Haszonkereső feladat: ha a piros úton mindig csak az éppen legnagyobb értéket választja, a mohó algoritmus nem biztos hogy megtalálja tényleg (abszolút) legnagyobb értéket (zöld út).

Gyengeség 2.:Analitikai értelmezés: Az "A" pontból indulva a mohó algoritmus az "m" felé fog törekedni. A nagyobb meredekség nem jelenti automatikusan a magasabb csúcsot.

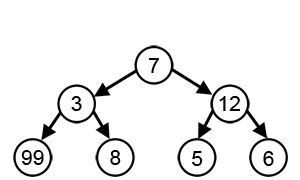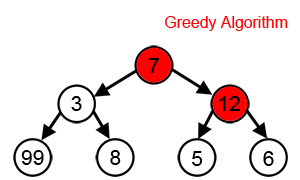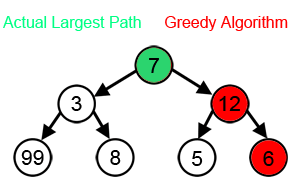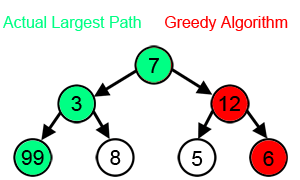
A mohó algoritmus vagy greedy algoritmus az a problémamegoldó algoritmus, amely helyi optimumok megvalósításával próbálja megtalálni a globális optimumot. Ez például az utazó ügynök problémájaként ismert feladatban azt jelenti, hogy minden állomásról a legközelebbi, addig még nem látogatott városba fog utazni az ügynök.

Általánosan öt pillérre támaszkodik:

• egy halmazból veszi a jelölteket, amelyekkel felállítja a megoldáshalmazt
• egy kiválasztó függvény, amely a legjobb jelöltet választja ki a megoldás reményében
• egy lehetőségvizsgáló függvény, amely megnézi, hogy egy jelölt alkalmas-e a megoldásra
• egy célfüggvény, amely egy értéket megoldásnak, vagy részleges megoldásnak jelöl
• egy megoldásfüggvény, amely jelzi, ha megtaláltuk a teljes megoldást.

A módszer jól alkalmazható néhány matematikai probléma megoldásában, de nem garantálja sok probléma megoldását.

Példák

• Az utazó ügynök problémájaként ismert feladat: Minden állomásról a legközelebbi, addig még nem látogatott városba utazva bejárni a városokat a legrövidebb útvonalon.
• Kruskal-algoritmus: Egy összefüggő gráf éleihez hozzárendelnek egy szigorúan pozitív számot, az úgynevezett költséget. Meg kell határozni a minimális feszítőfát a csúcsok között.
• Dijkstra-algoritmus: egy mohó algoritmus, amivel irányított vagy irányítás nélküli gráfokban lehet megkeresni a legrövidebb utakat egy adott csúcspontból kiindulva.

Alkalmazásai

A mohó algoritmusok igen jól teljesítenek ahol gyors és kis számítási kapacitású keresést kell megvalósítani, ellenben egyetlen megoldást adnak alternatívák nélkül. Bonyolult állapotterek esetén minimális javulást eredményezhetnek.

• Huffman-kódolás az adattömörítésben
• Erdős–Straus-sejtés a matematikában

Források

• Introduction to Algorithms (Cormen, Leiserson, and Rivest) 1990, 17. fejezet Greedy Algorithms 329. old.
• Introduction to Algorithms (Cormen, Leiserson, and Rivest) 2001, 16. fejezet Greedy Algorithms.
• G. Gutin, A. Yeo és A. Zverovich, Traveling salesman should not be greedy: domination analysis of greedy-type heuristics for the TSP. Discrete Applied Mathematics 117 (2002), 81-86.
• J. Bang-Jensen, G. Gutin and A. Yeo, When the greedy algorithm fails. Discrete Optimization 1 (2004), 121-127.
• G. Bendall and F. Margot, Greedy Type Resistance of Combinatorial Problems, Discrete Optimization 3 (2006), 288-298.

Fordítás

• Ez a szócikk részben vagy egészben a Greedy algorithm című angol Wikipédia-szócikk ezen változatának fordításán alapul. Az eredeti cikk szerkesztőit annak laptörténete sorolja fel. Ez a jelzés csupán a megfogalmazás eredetét és a szerzői jogokat jelzi, nem szolgál a cikkben szereplő információk forrásmegjelöléseként.

További információk

• Egyszerű példa a greedy algoritmushoz C++ nyelvben