Tetradekagon

Regular tetradekagon
Regular tetradekagon
	Sebuah tetradekagon sekata
Jenis	Poligon sekata
Sisi dan bucu	14
Simbol Schläfli	{14}, t{7}
Rajah Coxeter	;
Kumpulan simetri	Dihedral (D14), order 2×14
Sudut dalaman (darjah)	154+2/7°
Poligon duaan	Swapoligon
Sifat	Cembung, kitaran, sama sisi, isogonal, isotoksal

Tetradekagon biasa

Sisi dan bucu	14
Simbol Schläfli	{14}
Diagram Coxeter–Dynkin
Kumpulan simetri	Dwihedron(D₁₄)
Sudut dalaman (darjah)	180*(6/7) darjah $\simeq 154.2857$
Ciri-ciri	cembung, kitaran, sama sisi, isogon, isotoksal

Tetradekagon (atau tetrakaidekagon) ialah poligon dengan 14 sisi dan sudut.

Luas tetradekagon biasa dengan panjang sisi a ialah

A={\frac {14}{4}}a^{2}\cot {\frac {\pi }{14}}\simeq 15.3345a^{2}

Tetradekagon biasa

Tetradekagon sekata mempunyai simbol Schläfli {14} dan boleh dibina sebagai kuasi sekata dipotong heptagon, t{7 }, yang menggantikan dua jenis tepi.

luas sebuah sekata tetradekagon panjang sisi a diberikan oleh

A={\frac {14}{4}}a^{2}\cot {\frac {\pi }{14}}\approx 15.3345a^{2}

Pembinaan

Oleh kerana 14 = 2 × 7, tetradekagon sekata tidak boleh dibina menggunakan kompas dan garis lurus.^[1] Walau bagaimanapun, ia boleh dibina menggunakan neusis dengan menggunakan sudut trisektor,^[2] atau dengan pembaris bertanda,^[3] seperti yang ditunjukkan dalam dua contoh berikut.

Tetradekagon dengan *diberi bulatan*:
Animasi (1 min 47 s) daripada binaan neusis dengan jejari bulatan ${\overline {OA}}=6$ ,
menurut Andrew M. Gleason,^[2] berdasarkan pemasangan sudut melalui tomahawk.

Tetradekagon dengan *panjang sisi yang diberikan*:
Animasi (1 min 20 s) daripada binaan neusis dengan pembaris bertanda, menurut David Johnson Leisk (Crockett Johnson).^[3]

Simetri

Tetradekagon biasa mempunyai Simetri Dih₁₄, tertib 28. Terdapat 3 simetri dihedral subkumpulan: Dih₇, Dih₂, dan Dih₁ dan 4 kumpulan kitaran simetri: Z₁₄, Z₇, Z₂ dan Z₁.

8 simetri ini boleh dilihat dalam 10 simetri yang berbeza pada tetradekagon, jumlah yang lebih besar kerana garis pantulan boleh sama ada melalui bucu atau tepi. John Conway melabelkannya dengan surat dan susunan kumpulan.^[4] Simetri penuh bentuk biasa ialah r28 dan tiada simetri dilabelkan a1. Simetri dihedral dibahagikan bergantung kepada sama ada ia melalui bucu (d untuk pepenjuru) atau tepi (p untuk serenjang), dan i apabila garis pantulan melalui kedua-dua tepi dan bucu. Simetri kitaran dalam lajur tengah dilabelkan sebagai g untuk tertib pusingan pusatnya.

Setiap simetri subkumpulan membenarkan satu atau lebih darjah kebebasan untuk bentuk yang tidak teratur. Hanya subkumpulan g14 tidak mempunyai darjah kebebasan tetapi boleh dilihat sebagai directed edge.

Tetradekagon tak sekata simetri tertinggi ialah d14, sebuah tetradekagon isogonal yang dibina oleh tujuh cermin yang boleh berselang-seli tepi panjang dan pendek, dan p14, sebuah isotoxal tetradekagon, dibina dengan panjang tepi yang sama, tetapi bucu berselang seli dua sudut dalam yang berbeza. Kedua-dua bentuk ini adalah dwi antara satu sama lain dan mempunyai separuh susunan simetri tetradekagon biasa.

Pembedahan

unjuran 14-kiub.	84 belah ketupat

Coxeter menyatakan bahawa setiap zonogon (2m-gon yang sisi bertentangannya selari dan sama panjang) boleh dibedah menjadi m(m-1 )/2 segi empat selari.^[5] Khususnya, ini benar untuk poligon sekata dengan banyak sisi yang sama rata, dalam hal ini segiempat selari semuanya adalah rombi. Untuk tetradekagon biasa, m=7, dan ia boleh dibahagikan kepada 21: 3 set 7 romb. Penguraian ini berdasarkan unjuran poligon Petrie bagi 7-kubus, dengan 21 daripada 672 muka. Senarai Templat:OEIS2C mentakrifkan bilangan penyelesaian sebagai 24698, termasuk putaran sehingga 14 kali ganda dan bentuk kiral dalam pantulan.

Pembedahan kepada 21 belah ketupat

Penggunaan numismatik

Tetradekagon biasa digunakan sebagai bentuk beberapa syiling emas dan perak Malaysia, bilangan sisi mewakili 14 negeri Persekutuan Malaysia.^[6]

Figur berkaitan

The flag of Malaysia — Bendera Malaysia, menampilkan bintang berbucu empat belas

tetradekagon ialah poligon bintang 14 sisi, diwakili oleh simbol {14/n}. Terdapat dua poligon bintang biasa: {14/3} dan {14/5}, menggunakan bucu yang sama, tetapi menghubungkan setiap titik ketiga atau kelima. Terdapat juga tiga sebatian: {14/2} dikurangkan kepada 2{7} sebagai dua heptagon, manakala {14/4} dan {14/6} dikurangkan kepada 2{7/2} dan 2 {7/3} sebagai dua heptagrams berbeza, dan akhirnya {14/7} dikurangkan kepada tujuh digon.

Aplikasi yang ketara bagi bintang berbucu empat belas adalah dalam bendera Malaysia, yang menggabungkan tetradekagram {14/6} kuning di penjuru kanan sebelah atas, mewakili perpaduan tiga belas negeri dengan kerajaan persekutuan.

Sebatian dan poligon bintang
n	1	2	3	4	5	6	7
Bentuk	Regular	Kompaun	Poligon bintang	Kompaun	Poligon bintang	Kompaun
Imej	{14/1} = {14}	{14/2} = 2{7}	{14/3}	{14/4} = 2{7/2}	{14/5}	{14/6} = 2{7/3}	{14/7} or 7{2}
Sudut dalaman	≈154.286°	≈128.571°	≈102.857°	≈77.1429°	≈51.4286°	≈25.7143°	0°

Pemotongan yang lebih dalam bagi heptagon sekata dan heptagrams boleh menghasilkan bentuk tetradekagram perantaraan isogonal (vertex-transitive) dengan bucu yang sama jarak dan dua panjang tepi. Pemotongan lain boleh membentuk poligon penutup berganda 2{p/q}, yang ternama: t{7/6}={14/6}=2{7/3}, t{7/4}={14/4}=2{7/2}, dan t{7/2}={14/2}=2{7}.^[7]

Pemotongan isogonal heptagon dan heptagram
Kuasi sekata	Isogonal	Quasiregular Penutup berganda
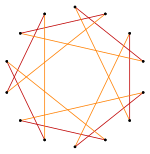
t{7}={14}		{7/6}={14/6} =2{7/3}
t{7/3}={14/3}		t{7/4}={14/4} =2{7/2}
t{7/5}={14/5}		t{7/2}={14/2} =2{7}

Bentuk isotoxal

poligon isotoks boleh dilabelkan sebagai {p_α} dengan sudut paling luar dalam α, dan poligon bintang {(p/q)_α}, dengan q ialah nombor penggulungan, dan gcd(p,q)=1, q<p. Tetradekagon isotoxal mempunyai p=7, dan kerana 7 ialah perdana semua penyelesaian, q=1..6, adalah poligon.

{7_α}	{(7/2)_α}	{(7/3)_α}	{(7/4)_α}	{(7/5)_α}	{(7/6)_α}

Poligon Petrie

Pencongan biasa tetradekagon wujud sebagai poligon Petrie untuk banyak politop berdimensi lebih tinggi, ditunjukkan dalam pencongan unjuran ortogon ini, termasuk:

Poligon Petrie
B₇		2I₂(7) (4D)
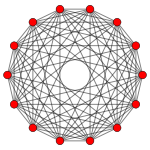7-ortopleks	7-kiub	7-7 duopiramid	7-7 duoprisme
A₁₃	D₈		E₈
13-simplex	5₁₁	1₅₁	4₂₁	2₄₁

Rujukan

^ Wantzel, Pierre (1837). "Recherches sur les moyens de Reconnaître si un Problème de géométrie peau se résoudre avec la règle et le compas" (PDF). Journal de Mathématiques: 366–372.
^ ^a ^b Gleason, Andrew Mattei (March 1988). "Angle trisection, the heptagon, p. 186 (Fig.1) –187" (PDF). The American Mathematical Monthly. 95 (3): 185–194. doi:10.2307/2323624. Diarkibkan daripada yang asal (PDF) pada 2016-02-02.
^ ^a ^b Weisstein, Eric W. "Heptagon." From MathWorld, A Wolfram Web Resource.
^ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275-278)
^ Coxeter, Mathematical recreations and Essays, Thirteenth edition, p.141
^ The Numismatist, Volume 96, Issues 7-12, Page 1409, American Numismatic Association, 1983.
^ The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Branko Grünbaum

Pautan Luar

Rencana berkenaan geometri ini ialah rencana tunas. Anda boleh membantu Wikipedia dengan mengembangkannya.

[1] Wantzel, Pierre (1837). "Recherches sur les moyens de Reconnaître si un Problème de géométrie peau se résoudre avec la règle et le compas" (PDF). Journal de Mathématiques: 366–372.

[Gleason-2] Gleason, Andrew Mattei (March 1988). "Angle trisection, the heptagon, p. 186 (Fig.1) –187" (PDF). The American Mathematical Monthly. 95 (3): 185–194. doi:10.2307/2323624. Diarkibkan daripada yang asal (PDF) pada 2016-02-02.

[Johnson-3] Weisstein, Eric W. "Heptagon." From MathWorld, A Wolfram Web Resource.

[4] John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, (2008) The Symmetries of Things, ISBN 978-1-56881-220-5 (Chapter 20, Generalized Schaefli symbols, Types of symmetry of a polygon pp. 275-278)

[5] Coxeter, Mathematical recreations and Essays, Thirteenth edition, p.141

[6] The Numismatist, Volume 96, Issues 7-12, Page 1409, American Numismatic Association, 1983.

[7] The Lighter Side of Mathematics: Proceedings of the Eugène Strens Memorial Conference on Recreational Mathematics and its History, (1994), Metamorphoses of polygons, Branko Grünbaum

[1]

[2]

[3]

[4]

[5]

[6]

[7]

l b s Poligon
Senarai berdasarkan bilangan sisi
1–10 sisi	Henagon (Monogon) · Digon · Segi tiga (Trigon) · Segi empat (Tetragon) · Pentagon · Heksagon · Heptagon · Oktagon · Nonagon (Enneagon) · Dekagon
11–20 sisi	Hendekagon · Dodekagon · Triskaidekagon · Tetradekagon · Pentadekagon · Heksadekagon · Heptadekagon · Oktadekagon · Nonadekagon (Enneadekagon) · Ikosagon
Lain-lain	Apeirogon
Poligon bintang	Pentagram · Heksagram · Heptagram · Oktagram · Enneagram · Dekagram · Hendekagram · Dodekagram